Nested Rubber Bands
The other day I came across a neat problem on the Codeforces round 633 div. 1. Go check out the problem statement and try thinking about it on your own!
I will assume a familiarity with the concepts of tree dynamic programming; if you haven’t encountered that topic yet this probably isn’t the best way to introduce yourself to the topic.
Since this is my first blog post, I’m not sure exactly how I’ll format things, but for now I’ll just step through my code.
The way we’ll solve this problem is by constructing two dp tables as follows:
dpIn[node] represents the maximum number of vertices we can use for our selected nesting, if we are only using nodes from this subtree, and this node may be used (note that it might be that we don’t use this node, despite the name “dpIn”, since any answer can be constructed with this node selected could also happen if it weren’t so, in the off-case where it might be better to select a ton of children, rather than select our node, we must also take the possibility of not taking this node.
dpOut[node] is the same, but requires you to not include this node.
To illustrate this idea better, let’s look at how the answers might be formed using this scheme. The optimal answer can occur via 2 cases:
Case 1. Straight path
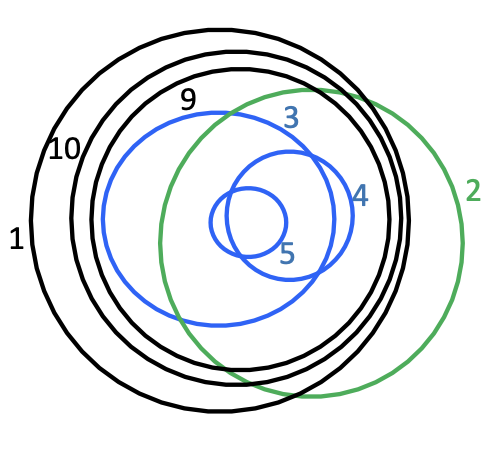
It is a straight down path beginning from a specific node (pretend we reroot the tree so the current node is the root). A path is a line of nodes that we pass through, and as we go through this line I can collect this node as part of our nesting, then skip a node, or I can take the children on a layer except for one, and recurse onto that one.
In the case below: I can take the top node, skip a layer, then take the nodes of 3rd layer except for the first. Then, I recurse there and decide to take that 3rd layer’s first node, and recurse on children, and terminate since there are none. (You should test this out on paper to convince yourself that it works)
In this case, the path was from the top-left to the bottom left node.
Case 2. Combine two paths
This is quite hard to see, but let’s go through the case where we combine two paths that begin an excluded node (dpOut):
Case 2a. Two paths both begin with an exclusion
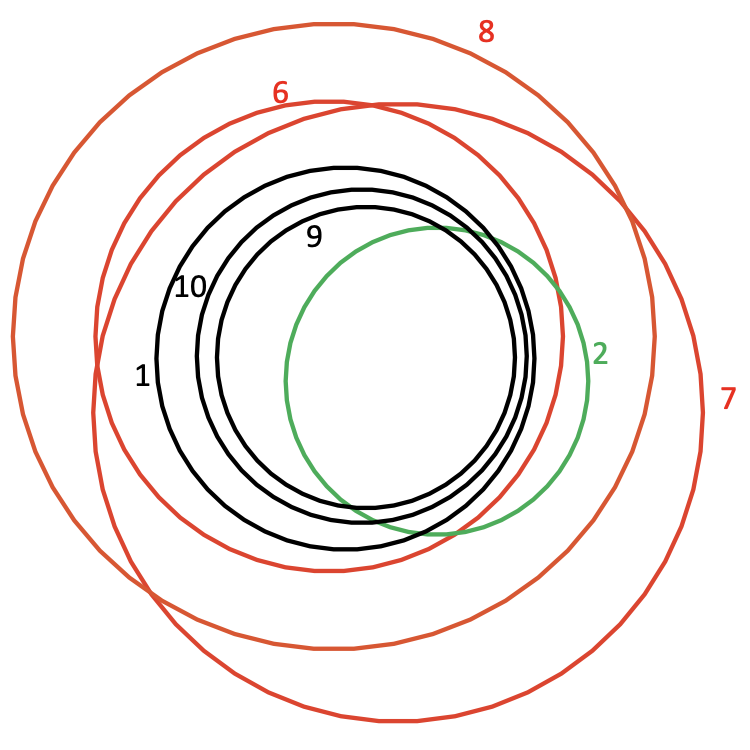
Here, we should take combine the two paths: [a], and [b]. Even though they’re single nodes, we use the node R as the start of our nesting. If you draw it out, you can see that we can use the 3 children of a to be “inside” of the root R and the 3 children of b to be “outside” of the root.
So, if we added extra neighbors of R, we could actually nestle them between the a and b constructions, but we couldn’t use any other paths, because we’ve essentially used up the two possible topological regions available.
But we can fit any number of neighbors between them (this includes children and parent). Or, if a and b are our only children, we can just use R.
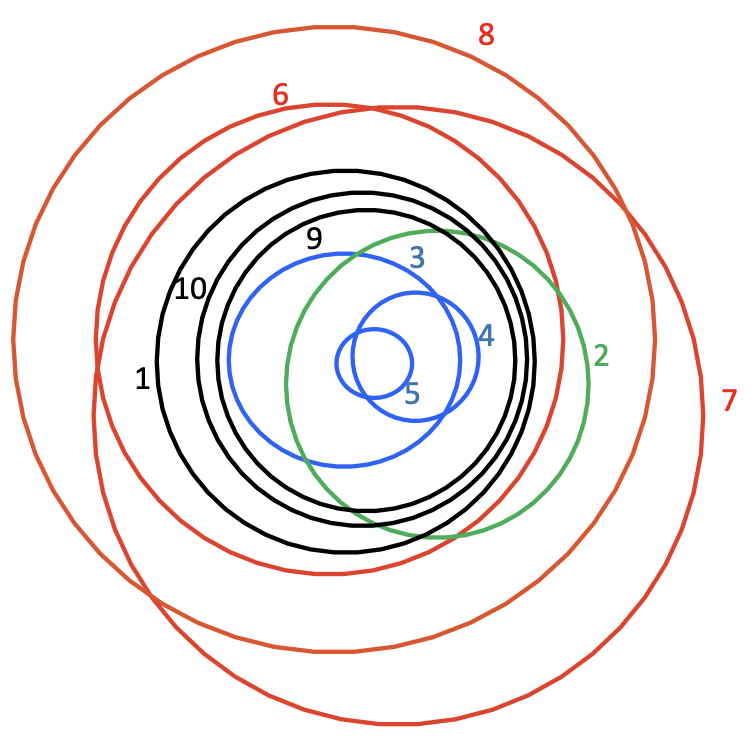
Case 2b. Two paths both begin with an inclusion
In this example, we are combining paths from child a and child b. Here, you can draw out the same concept, where we can use child a to be “inside” of R’s rubber band, and b is “outside.” Then, any remaining children, c1, c2,.. as well as the parent, P, may be included by “sandwiching” them in between.
In case this still isn’t clear, here’s a rought drawing of the three cases I just described.
Inside Case: Blue, and any number of black can go between the outside blue and inside green, sandwiched between.
Outside Case: Red, and any number of black can go outside green and inside red, sandwiched between.
Combined Case: Notice that we cannot rely on more branches similar to the red and blue ones, because topologically, there are only two spaces: inside and outside. We physically cannot fit anything else!
Below is the bulk of the code for the problem. We call the solve function on any arbitrary node and we will update best to be the maximum nesting depth possible.
static ArrayList<Integer>[] adjList;
static int[] dpIn, dpOut;
static int best;
static void solve(int node, int par) {
dpIn[node] = 1; // We begin by taking ourself (base case is we are a leaf)
int size = adjList[node].size() - (par != -1 ? 1 : 0);
dpOut[node] = size; // we can always just take all our neighbors and stop
// When we construct our global answer, we need to potentially combine
// two paths. This part is very topological and tricky, not sure how to prove.
// But essentially, it seems like we can
int path1In = 0;
int path2In = 0;
int path1Out = 0;
int path2Out = 0;
for (int adj : adjList[node]) {
if (adj != par) {
solve(adj, node); // get the values for the children, now let's use them
// If we exclude this node, then we take all the children, and then
// we use one of the nodes to extend the path further!
dpOut[node] = Math.max(dpOut[node], size - 1 + dpIn[adj]);
// As stated above, our dpIn[node] can either include the node we're
// at, in which case we get our node, and now, to build our path,
// we try going down one of our children and using a path that leaves
// a gap in the rubberbands (they need to alternate)
dpIn[node] = Math.max(dpIn[node], 1 + dpOut[adj]);
// Also, a path that excludes this node is only less restrictive,
// so we can safely use that as the path through this node without
// violating anything!
dpIn[node] = Math.max(dpIn[node], dpOut[node]);
// Now, what we do here is repeatedly push out the optimum answer for
// the 1st place and 2nd place paths seen. If we beat the first,
// then the second can take the first val, the first takes the new val.
// If it only beats the second, then the second takes the new val.
if (dpOut[adj] > path1Out) {
path2Out = path1Out;
path1Out = dpOut[adj];
}
else if (dpOut[adj] > path2Out) {
path2Out = dpOut[adj];
}
if (dpIn[adj] > path1In) {
path2In = path1In;
path1In = dpIn[adj];
}
else if (dpIn[adj] > path2In) {
path2In = dpIn[adj];
}
}
}
// Of course, we maximize our answer with the single path case
best = Math.max(best, dpIn[node]);
best = Math.max(best, dpOut[node]);
// Combining two paths:
int addPar = (par != -1 ? 1 : 0);
best = Math.max(best, Math.max(1, size - 2 + addPar) + path1Out + path2Out);
best = Math.max(best, size - 2 + addPar + path1In + path2In); // path through us as an unused node
}
Thanks for reading! Hopefully this was useful!